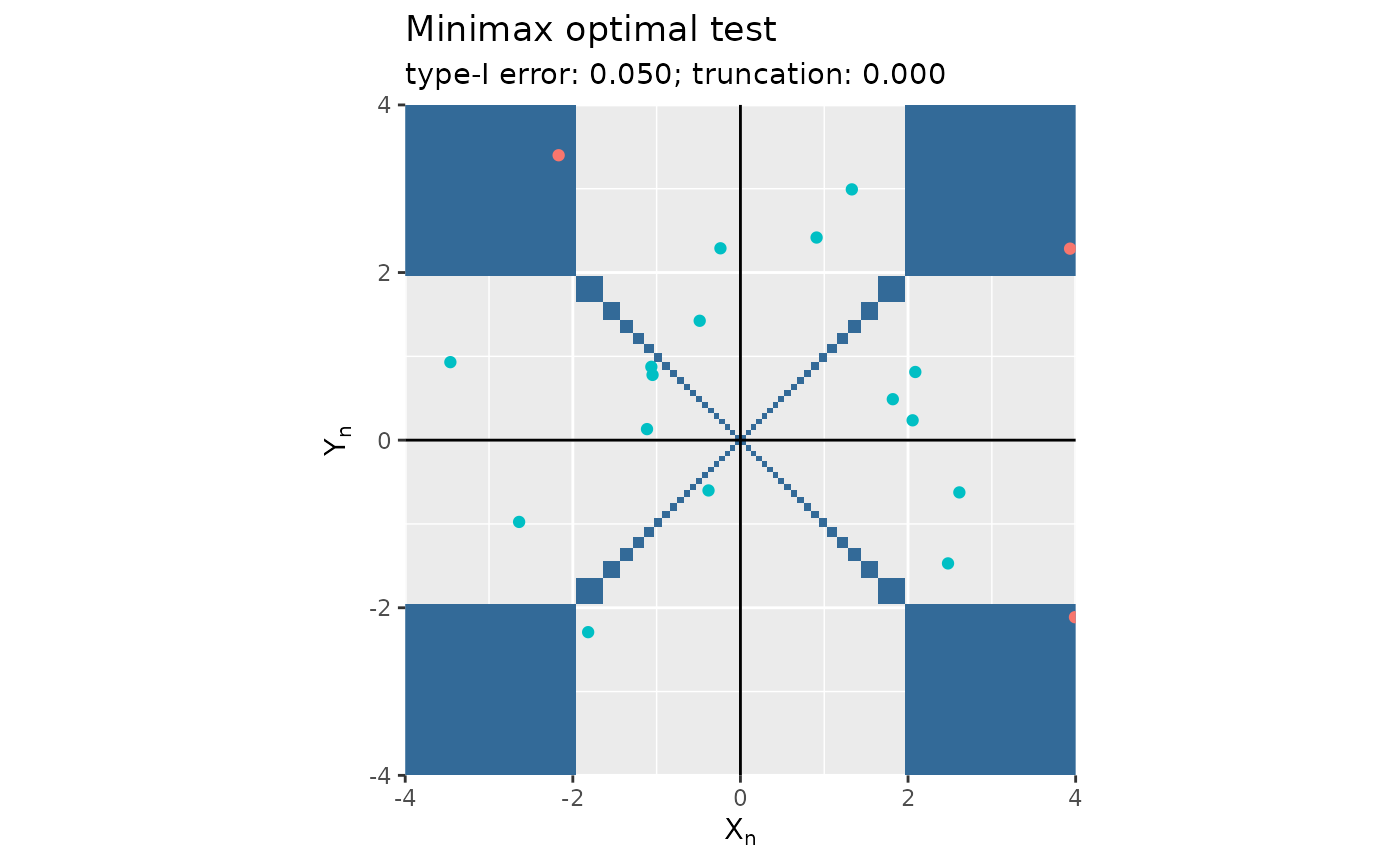
Minimax optimal testing

Carries out the minimax optimal test of the composite null "\(\delta_x \times \delta_y=0\)" against its alternative "\(\delta_x \times \delta_y\neq 0\)" based on the test statistic in the real plane.

Usage

mediation_test_minimax(
  t,
  alpha = 0.05,
  truncation = 0,
  sample_size = Inf,
  compute_pvals = TRUE
)

Arguments

t

A vector consisting of two numerics, the test statistic in the real plane, or a 'n x 2' matrix of such test statistics.

alpha

A positive numeric, the wished type-I error.

truncation

A nonnegative numeric used to bound the rejection region away from the null hypothesis space. Defaults to 0, in which case the rejection region is minimax optimal.

sample_size

An integer (larger than one), the size of the sample used to derive the test statistic. Defaults to 'Inf', meaning that, under the null hypothesis, the test statistic is drawn from the \(N_2(0,I_2)\) law. If the integer is finite, then, under the null hypothesis, the test statistic is drawn from the product of two Student laws with 'sample_size-1' degrees of freedom.

compute_pvals

A logical indicating whether or not (conservative) p-values should be computed.

Value

A list, consisting of:

t:

a vector of two numerics, the test statistic, or a 'n x 2' matrix of such test statistics;

alpha:

a numeric, the type-I error;

truncation:

a nonnegative numeric, used to bound the rejection region away from the null hypothesis space

sample_size:

an integer, the size of the sample used to derive the test statistic

decision:

a vector of logicals, FALSE if the null hypothesis can be rejected for the alternative at level 'alpha' and TRUE otherwise;

pval:

a vector of numerics, the (conservative) p-values of the tests;

method:

the character "minimax".

Details

For details, we refer to the technical report "Optimal Tests of the Composite Null Hypothesis Arising in Mediation Analysis", by Miles & Chambaz (2024), https://arxiv.org/abs/2107.07575

See also

mediation_test_minimax_BH(), which builds upon the present function to implement a Benjamini-Hochberg procedure to control false discovery rate.

Examples

n <- 10
x <- MASS::mvrnorm(2 * n, mu = c(0, 0), Sigma = diag(c(1, 1)))
delta <- matrix(stats::runif(4 * n, min = -3, max = 3), ncol = 2)
epsilon <- stats::rbinom(n, size = 1, prob = 1/2)
delta <- delta * cbind(c(epsilon, rep(1, n)),
                       c(1 - epsilon, rep(1, n)))
x <- x + delta
(mt <- mediation_test_minimax(x, alpha = 1/20))
#> Testing the composite null 'delta_x * delta_y = 0' against its alternative 'delta_x * delta_y != 0':
#> * method:
#> minimax 
#> * test statictic:
#>            [,1]       [,2]
#> [1,] -2.6409670 -0.9758506
#> [2,]  2.6123343 -0.6235647
#> [3,] -1.1148832  0.1316706
#> [4,]  1.8182577  0.4886288
#> [5,]  0.3819511 -4.4230687
#> [6,]  2.4769649 -1.4707363
#> ...
#> * wished type-I error:
#> [1] 0.05
#> * user-supplied truncation parameter:
#> [1] 0
#> * size  of the sample used to derive the  test statistic ('Inf' to use a Gaussian approximation; otherwise, use a product of Student laws):
#> [1] Inf
#> * decision [3 rejection(s) overall]: 
#> cannot reject the null for its alternative with confidence 0.050
#>  cannot reject the null for its alternative with confidence 0.050
#>  cannot reject the null for its alternative with confidence 0.050
#>  cannot reject the null for its alternative with confidence 0.050
#>  cannot reject the null for its alternative with confidence 0.050
#>  cannot reject the null for its alternative with confidence 0.050
#> ...
#> * (conservative) p-value:
#> [1] 0.3291385 0.5329135 0.8952448 0.6251045 0.7024976 0.1413624
#> ...
plot(mt)
#> Some points fall outside the range of the figure.