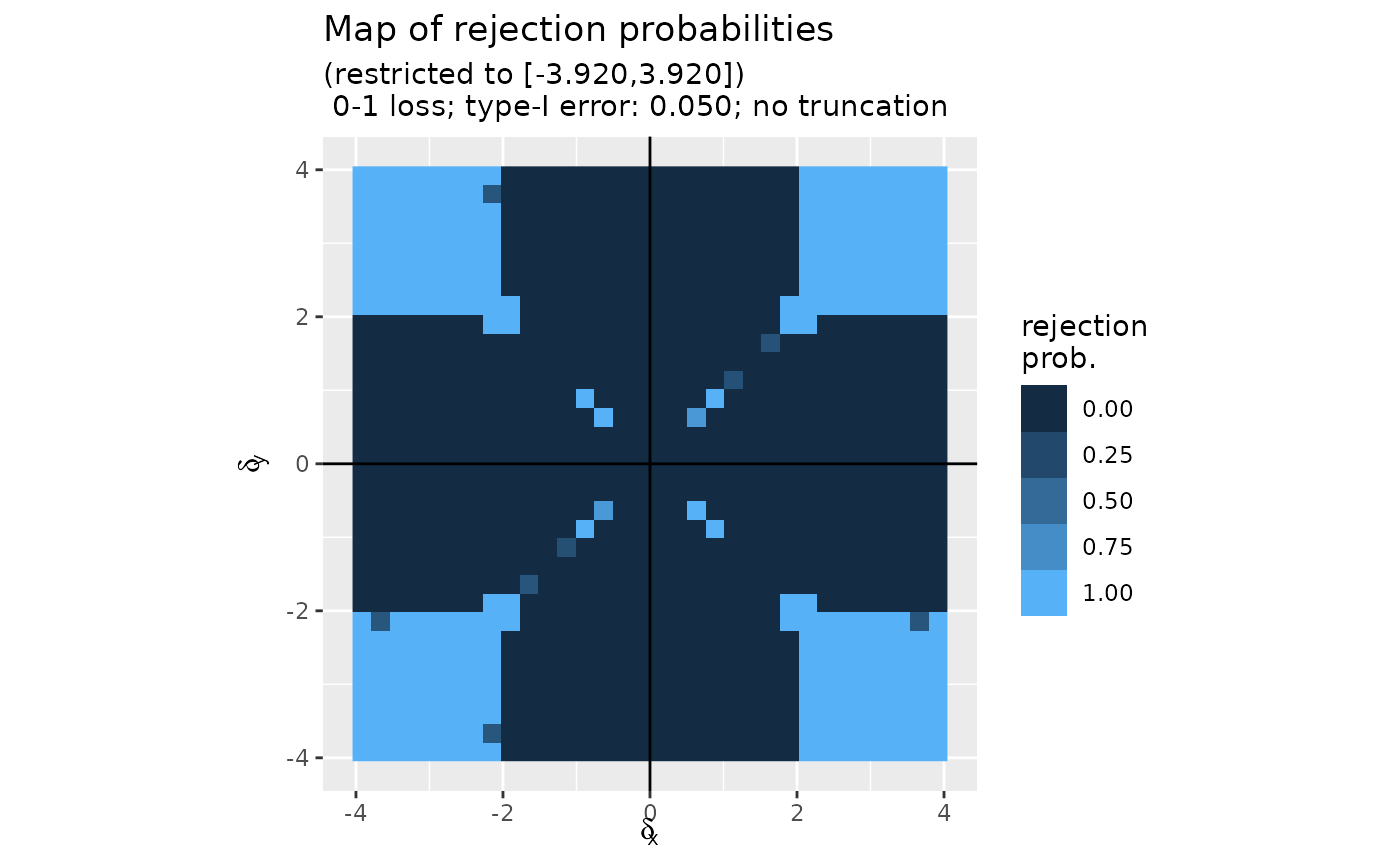
Computing 'map's of rejection probabilities for the Bayes risk optimal test

Computes the "map" of rejection probabilities for the Bayes risk optimal test of the composite null "\(\delta_x \times \delta_y=0\)" against its alternative "\(\delta_x \times \delta_y\neq 0\)" based on the test statistic in the real plane. The Bayes risk is induced by either the 0-1 or the bounded quadratic loss function, a wished type-I error and, possibly, a truncation parameter.

Usage

compute_map_rejection_probs(
  alpha = 0.05,
  K = 16,
  loss = c("0-1", "quadratic"),
  sample_size = Inf,
  truncation = 0,
  return_solver = FALSE
)

Arguments

alpha

A positive numeric, the wished type-I error (default value 0.05).

K

An integer parametrizing the discretization of the null hypothesis test and of the plane. The complexity of the resulting optimization problem is \(O(K^2)\), so 'K' should neither be too small nor too large. The default value is 'K=16'. We recommend 'K=64' as a sensible value and enforce \(2 \le K \le 128\).

loss

A character, either "0-1" (default value) or "quadratic", to indicate which loss function to consider.

sample_size

An integer (larger than one), the size of the sample used to derive the test statistic. Defaults to 'Inf', meaning that, under the null hypothesis, the test statistic is drawn from the \(N_2(0,I_2)\) law. If the integer is finite, then, under the null hypothesis, the test statistic is drawn from the product of two Student laws with 'sample_size-1' degrees of freedom.

truncation

A nonnegative numeric, enabling to bound away the rejection region from the null hypothesis space. Its default value is 0, meaning that no truncation is required.

return_solver

A logical, to request that the 'lpSolve' object be returned (if 'TRUE') or not (if 'FALSE', default). Note that the 'lpSolve' object can be quite big.

@return A '2K x 2K' matrix whose '(i,j)' coefficient is the probability to reject the null when the test statistic falls in the square \([b(i-1-K)/K, b(i-K)/K] \times [b(j-1-K)/K, b(j-K)/K]\), with 'b' set to '2 * stats::qnorm(1 - alpha / 2)'. If 'return_solver' is 'TRUE', then the matrix has an attribute called 'solver' which is the complete output of the optimization function 'lpSolve::lp' used to determine the probabilities.

Examples

## one of the nine outputs of 'compute_map_rejection_probs' stored in the package
head(map_01_0.05, c(5, 5)) 
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    1    1    1    1
#> [2,]    1    1    1    1    1
#> [3,]    1    1    1    1    1
#> [4,]    1    1    1    1    1
#> [5,]    1    1    1    1    1
map <- compute_map_rejection_probs(alpha = 0.05, K = 16, loss = "0-1")
plot(map)